Hokm is a 4-player Persian card game similar to Bridge, and the robot is learning it by playing against younger versions of itself!

Introduction

So far, all the games I’ve modeled using Reinforcement Learning, from OpenAI Gym and Atari to my recent project on teaching LLMs to play text-based games, were single-player, perfect-information environments. To learn more about RL and tackle a more challenging problem, I decided to take on a multi-agent, imperfect-information game. I chose Hokm, a famous Persian card game, which I personally very much enjoy!

What makes this project unique is that it’s the first time—that I know of—that anyone has tackled solving Hokm using reinforcement learning. The game presents fascinating challenges: 4-player partnerships, hidden information, and the need for silent collaboration where teammates can’t communicate directly. It’s most similar to games like Bridge, Spades, Hearts, and even the Swiss game of Jass, with teams competing to win 7 out of 13 tricks (I have a full descriptions of the game and its rules in the Appendix section).

If you know Hokm, and you are curious how the trained model performs, check out the appendix for a sample game evaluation.

Code repository link will be added after cleanup.

Why Hokm is Perfect for Multi-Agent RL Research

Hokm presents several computational challenges that make it an ideal test case for advanced RL research:

Imperfect Information: With 39 cards hidden initially—13 in each opponent’s hand and 13 in your partner’s hand—the space of possible game states is enormous. Effective play requires continuous belief updating as information is revealed through played cards.

Random card dealing: No two games are identical. Random card distribution ensures that initial dealing significantly influences game outcomes, adding layers of uncertainty that pure strategy cannot overcome.

Partnership Coordination: Success demands seamless coordination with a teammate whose hand and intentions remain opaque. This creates a unique multi-agent learning problem where cooperation and competition must coexist in delicate balance.

Strategic Complexity: The interplay between individual trick-taking tactics and partnership coordination creates a decision space that resists simple heuristic approaches. The game rewards both short-term tactical acumen and long-term strategic vision.

Methodology

Environment Design

Fresh from developing a PPO solution for text-based games, I had a clear mental map of required components and potential code reuse opportunities. My first step involved crafting a detailed implementation plan—a concrete roadmap that proved invaluable for systematic progress and effective collaboration with LLMs during development.

Initially, I estimated 1-2 weeks to reach code completion and training readiness, but I achieved this in just two days, producing 6,000 lines of code with LLM assistance. Without this partnership, the timeline would have stretched into multiple weeks.

The first challenge was to write a custom environment for Hokm that was well-suited for an RL application. The environment’s role is to manage the game’s state, including shuffling the deck, dealing cards, and tracking tricks won, and to enforce game rules by providing legal actions to the agent. Crucially, it provides the observations and rewards—the feedback loop—that allows the agent to learn the optimal strategy for winning the game. I opted to use a heuristic for trump suit selection. In the next version, I can add that as a learning component for the model, but to simplify, I opted for this approach.

A crucial implementation detail involved dual player naming conventions. I maintained PLAYER_0 through PLAYER_3 for storage, evaluation, and reporting, while using AGENT, RIGHT, FRONT, and LEFT for feature representation during gameplay. This dual system proved essential for leveraging game symmetry, which simultaneously simplified and complicated implementation and modeling challenges.

Evaluation Strategy

Model evaluation diverged sharply from single-player scenarios. In single-player games, cumulative discounted rewards provide clear performance metrics. However, multi-player self-play creates a different dynamic—agents achieve roughly 50% win rates against themselves by definition. To track training progress, I developed two benchmark opponents: a random policy executing random legal moves, and a heuristics-based player following basic Hokm heuristics. The heuristic agent defeats the random player over 70% of the time, establishing a meaningful performance ladder.

League Training Architecture

Single-player RL follows a straightforward pattern: agents play against environments that provide rewards, with the goal of maximizing cumulative long-term discounted rewards. The environment for Hokm is merely a game container managing rules, turn sequences, and state transitions. So how could I train the agent?

My initial instinct pointed toward pure self-play—let agents battle themselves, collect rollouts, and update policies. This approach failed spectacularly. I couldn’t surpass 50% win rates against random opponents, achieving no meaningful learning. After literature review and reflection, the problem became clear: imagine training a tennis player through pure self-play. If you collect experiences from both sides and train a single model, it lacks incentive to improve either strengths or weaknesses—enhancement in either direction would harm its self-scoring ability. The result? A fragile policy that exploits its own weaknesses for victories but crumbles against any external opponent. Classic tail-chasing behavior.

Instead, I adopted a proven multi-agent RL strategy: competing against “frozen” model versions. I constructed a fixed-size league initially populated with the untrained model. After every five training iterations, I conducted arena tournaments where the learning model played 1,024 games against each frozen opponent. When the learning model achieved 52% victory rates, I froze it, added it to the league, and continued training. Full leagues triggered the removal of oldest models, creating a dynamic opponent pool reminiscent of AlphaStar’s approach.

Hardware-wise, I continued using my $300 RTX 3060 setup from previous projects. Unlike earlier work, memory constraints posed no issues thanks to the relatively modest model size requirements.

PPO Adaptation for Multi-Agent Environments

PPO employs an actor-critic architecture where the critic trains alongside the actor, helping estimate action quality through value functions and advantage estimation via Generalized Advantage Estimation (GAE). For deeper technical details, see the excellent Hugging Face explanation.

The advantage function quantifies how much better an action performs compared to the average action at that state. GAE estimates this advantage by combining multiple TD errors with exponentially decaying weights:

\[\hat{A}_t = \sum_{l=0}^{\infty} (\gamma\lambda)^l \delta_{t+l}\]

where TD error follows:

\[\delta_t = r_t + \gamma V(s_{t+1}) - V(s_t)\]

Multi-agent scenarios introduce a critical modification. Standard TD error calculation uses the next state’s value, $V(s_{t+1})$. However, in Hokm, the next state typically belongs to an opponent (except when the current player or teammate wins tricks). Since Hokm operates as a zero-sum game where one team’s +1.0 reward translates to the opponent’s -1.0 reward, opponent values require negation. This yields the modified TD error:

\[\delta_t = r_t + \sigma_t \gamma V(s_{t+1}) - V(s_t)\]

where $\sigma_t = -1$ when the next state belongs to opponents, and $+1$ for player or teammate turns. This crucial adjustment enables effective learning in zero-sum environments.

Another key decision involved using identical policies for same-team players. This approach yields dual benefits: learned cooperation and simplified learning/testing processes.

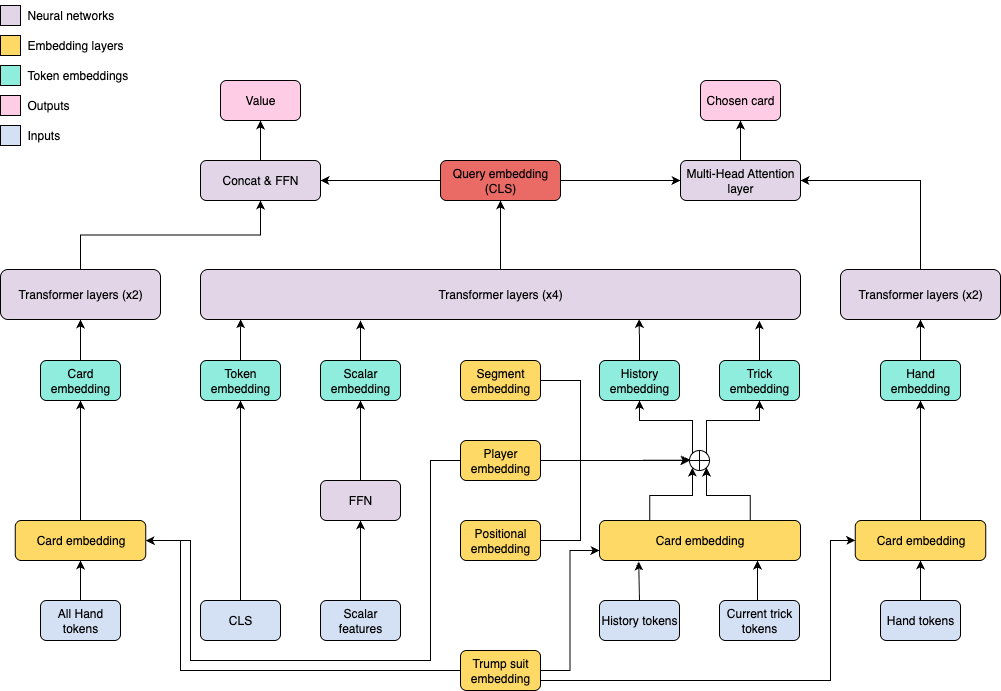
Model Architecture

The model implements a bespoke Transformer-based Actor-Critic that selects optimal cards (Actor) while estimating current game state value (Critic). Though seemingly complex, the architecture follows a clear logic:

We begin by processing public information across three categories:

Scalar features: Primarily game score tracking
Game history: Complete record of played cards across previous tricks
Current trick: Cards played in the ongoing trick

This information feeds into a 4-layer Transformer, with the CLS token’s embedding serving as our public_query vector. The Actor uses this query via pointer network architecture to examine the agent’s hand and select cards—far more efficient than guessing from all 52 cards while ensuring legal move selection. The Critic leverages the same query to evaluate all hands and generate value scores.

One important design note: the Critic operates as a “privileged” component with access to all hands. While this seems like cheating, the critic serves only training purposes, providing learning signals to the actor without influencing gameplay decisions. Superior critics enable easier training—a standard practice in multi-agent RL.

Additional architectural details appear in the appendix.

The Breakthrough: Layering Context

I must highlight one critical design breakthrough. Initially, I treated game state as simple sequences, using separator tokens like [TRICK] or [AGENT] to structure data. Performance was disappointing—the model struggled to connect cards with their contexts.

The transformation came through additive contextual embeddings. Rather than merely marking boundaries, this technique infuses every card with multiple information layers. Each card’s base representation receives enhancement through:

Segment embeddings: Distinguishing game history from current trick
Player embeddings: Identifying card owners—self, partner, or opponents
Status embeddings: Marking trump cards

This change proved transformative. The most intuitive way to understand its impact is geometrically. Imagine all the cards represented as points in a vast, multi-dimensional space (256-dim in this case). Without layered context, these points are relatively undifferentiated. The model has to learn the significance of each card from scratch.

Adding contextual embeddings is like drawing clear boundaries in this space, actively learning to partition the cards based on their strategic roles.

The ‘trump’ embedding pulls all the trump cards into a distinct region.
The ‘player’ embedding separates the cards into clusters based on who played them—one for you, one for your partner, and others for your left and right opponents.

Suddenly, the model isn’t just seeing a card’s identity (e.g., Ace of Spades); it’s seeing its strategic location. A trump card played by your partner now occupies a unique, pre-defined neighborhood in this geometric space, far from a non-trump card played by an opponent.

This direct injection of learned knowledge is incredibly efficient. The model doesn’t waste resources discovering these fundamental relationships; they are embedded directly into the geometry of the input. This frees up the model’s attention to focus on what truly matters: learning higher-level, nuanced strategy.

Training Protocol

The training algorithm follows this sequence:

Randomly initialize the model
Copy, freeze, and add the model to the league
Sample frozen opponents from the league
Collect N rollouts through opponent gameplay
Calculate advantages using modified TD error
Execute 4 PPO training rounds and update networks
Return to step 3

Every 5 iterations, the learning model competes against all league opponents across M games. Achieving collective 52% win rates earns league admission. Full leagues trigger oldest model removal.

Results and Analysis

Training Progress

Proper model evaluation requires competition against non-learning opponents. Here are average win rates from 1024 games played against random and heuristic opponents every 5 iterations throughout training:

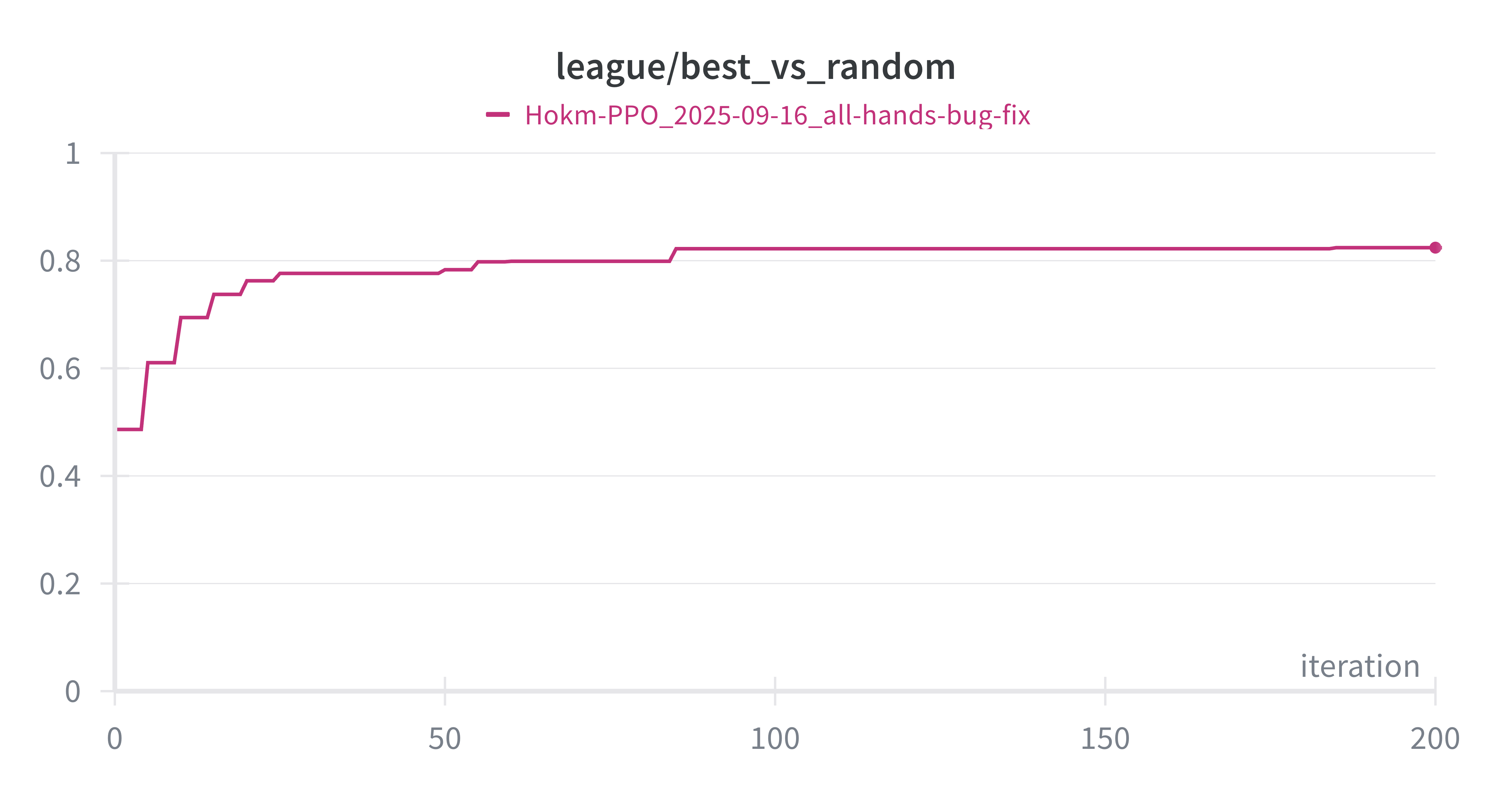
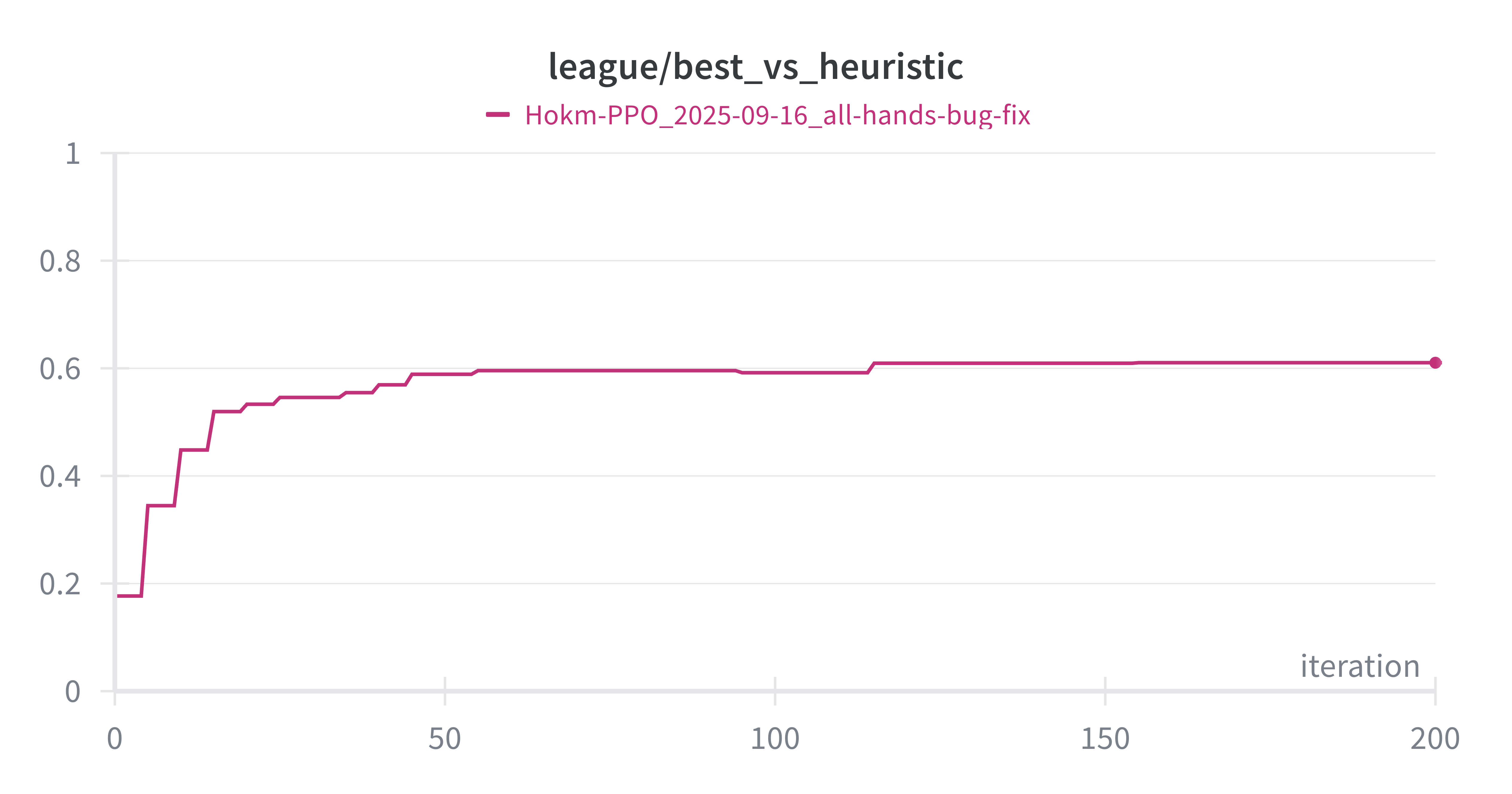
The model begins at random performance levels—50% against random opponent and approximately 20% against heuristic player. Performance climbs to over 80% and 60%, respectively. This may not seem impressive, but Hokm is a game that is highly decided by the initial card dealings, as apparent by how accurate the value function can predict the outcome right after dealing the cards. Think about it this way: if your hand is stacked with high cards, and is empty of one or more suits, even a random play would bring out those high cards, and they would win anyways. Also, usually a match is 7 games, and the expected value of winning a match against random and heuristic-based player would be around 80% and 99%, respectively (calculated from cumulative binomial distribution).

Value Function Learning

Let’s also look at how the value function is trained. Here is a graph of expected value during training:

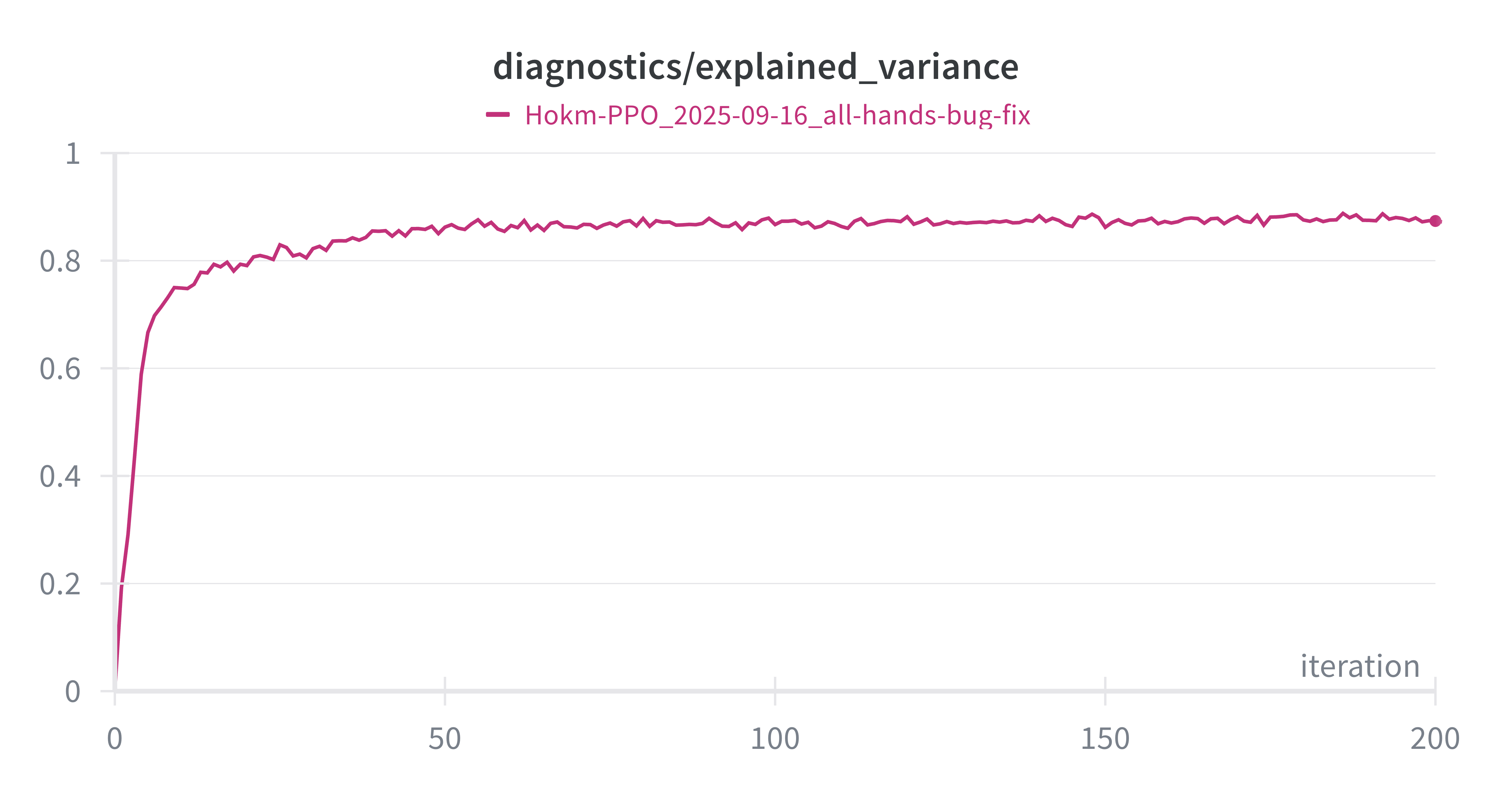
I’ve explained what expected value is in my last post, and how important it is to measure and monitor during training, but in short, it explains the variance in the data that is explained by the model. So a perfect model is going to have EV of 1.0, a model that outputs the average will have EV of 0.0, and a model that is working against you will have unbounded negative EV. Here we see that the critic quickly gets trained to achieve an impressive 0.88 within just 100 iterations.

Another interesting thing to look at is how good the value function is in predicting the outcome of the game, right after the dealing. Remember that the critic is privileged, so it sees all hands. A good value function should have a roughly good estimate of the chances of a team winning, just by looking at the cards, and knowing the trump suit. In this case, we are getting around 50% positive correlation between the initial estimation, and final outcome of the game. It shows that 1) initial card dealing is a highly important factor in the outcome of the game (explaining why even with random opponent, it is not possible to have 100% winrate), 2) the actual gameplay is important, especially in edge cases, 2) there is probably some room for improvement for both the policy and the value function.

Strategic Capabilities Analysis

One of my motivations for this project was to find out whether the trained model develops strategic thinking and heuristics, paralleling human expertise. While comprehensive analysis remains pending, preliminary game examination reveals promising patterns (though this doesn’t mean that the model is perfect now, as it still makes mistakes).

The trained model appears to demonstrate sophisticated, multi-layered Hokm strategy understanding, consistently executing what seem to be expert-level plays across several key domains. Here are some findings, with examples from a game presented in the Appendix.

Advanced Partnership Coordination

The model’s most impressive capability appears to lie in intelligent, non-obvious teamwork that transcends selfish trick-winning behavior to maximize team advantage.

Evidence: In Trick #2, Player 2 held the controlling Ace of Hearts but chose the 7H, allowing its partner’s Queen to win.

Significance: This “ducking” maneuver exemplifies advanced play. The AI correctly deferred trick-winning to preserve its Ace, trusting partner leadership while ensuring team suit control for future exploitation. This demonstrates learned theory of mind and strategic deference.

Dynamic Strategy and Advantage Leverage

The AI exhibits what seems to be keen game state and score awareness, dynamically shifting from information gathering to aggressive, game-ending plays.

Evidence: Holding a 4-0 lead in Trick #5, Player 2 correctly identified the moment to press advantage by leading the trump Ace.

Significance: This “bleeding trump” strategy optimally neutralizes opponent trump cards when ahead. The model’s critic value rose consistently afterward, reflecting accurate assessment of growing victory probability.

Logical Inference and Multi-Trick Planning

The model appears to make logical deductions from previous actions, planning moves across multiple tricks.

Evidence: In Trick #3, Player 0 led the King of Hearts with 89.51% confidence, making this play only after its Queen won the previous trick—potentially inferring that partner Player 2 held the Ace. This is what a human player would do.

Significance: This suggests hidden information tracking and belief updating, enabling safe “cashing out” of winners in proper sequence.

High-Stakes Execution

The model maintains composure and executes what appear to be optimal plays during critical, game-deciding moments.

Evidence: In the final trick, Player 3’s defensive trump (Queen of Diamonds) attempt to prevent 7-0 loss met Player 0’s higher trump (King of Diamonds) “overruff” with 99.98% policy confidence.

Significance: The model successfully navigated complex, multi-layered interactions at the game’s most crucial juncture, securing maximum possible scoring.

The model appears to transcend mere rule mastery to become a strategic, collaborative agent capable of executing nuanced, expert-level tactics that seem to mirror sophisticated human play.

Next steps

While I’m thrilled with the current results, this was just based on two weeks of work. There are several exciting directions to take this project next:

Teaching it to choose the Hokm/trump suit: Right now, the model uses a simple heuristic to pick the trump suit. The next major challenge is to make trump selection part of the learning process. This is an important strategic decision in the game, and teaching the AI to make that call will be a huge leap forward.
Deeper Strategic Analysis: I’ve only done a preliminary analysis of the gameplay. I could run a much larger-scale evaluation to really codify the agent’s emergent strategies. I could build a full “playbook” of its tactics and see how they stack up against human expert strategies.
Human-in-the-Loop: I’m really curious to see how the agent performs with a human partner. Can it adapt its collaborative strategies to a player who doesn’t think exactly like it does? This would be the ultimate test of its learned cooperative behavior.
Code Release & demo: After a bit more cleanup, I’ll be releasing the entire project—the custom environment, the training code, and the final models. I could also build a simple web-based demo so anyone can play against the AI.
Is this publishable? If I get the time, and add more to the analysis and training process, I’m wondering whether this might be suitable for submission to a conference. What do you think?

What I Learned

What I learned personally from this was massive. Moving from single-player environments to a multi-agent game felt like jumping from 2D to 3D. It’s not just a harder problem; it’s a fundamentally different one. I learned the hard way that the stability of the training setup is paramount. The “moving target” problem, where every agent is learning simultaneously, is no joke, and designing the league system wasn’t just an enhancement—it was the only way to make progress. It also hammered home how critical data representation is. The switch to contextual embeddings showed me that a clever architecture can be more impactful than just throwing more compute at a problem. This project has been a fantastic lesson in the nuances of multi-agent dynamics, and I’m excited to apply these insights to even more complex challenges.

Summary

This project was a deep dive into a multi-agent, imperfect-information game, and the results were awesome. I successfully built and trained an AI agent to play Hokm using multi-agent reinforcement learning, specifically PPO. The biggest hurdle was creating a stable training environment; pure self-play was a spectacular failure, leading to classic tail-chasing behavior. The solution was a league-based training system, where the agent constantly competed against a pool of “frozen” older versions of itself, forcing it to genuinely improve rather than just exploit its own weaknesses.

The model itself is a bespoke Transformer-based Actor-Critic, and the real breakthrough came from using additive contextual embeddings. This change was transformative, allowing the model to grasp the strategic significance of each card in context. The final agent achieves an 80% win rate against a random player and 60% against a heuristics-based one. But the coolest part isn’t the win rate; it’s seeing the AI develop what appear to be sophisticated, human-like strategies on its own—intelligent partner coordination, dynamic advantage pressing, and logical inference. It didn’t just learn the rules; it learned to play.

Appendix

I. The Game of Hokm

Overview

Hokm (Persian: حکم, meaning “command” or “rule”) is a sophisticated trick-taking card game that has been a cornerstone of Persian social gaming for generations. Played by four players arranged in partnerships, Hokm combines elements familiar from Western trick-taking games with unique mechanics that create rich, dynamic gameplay requiring both individual skill and partnership coordination.

Comparative Analysis with Other Trick-Taking Games

Understanding Hokm’s place in the broader family of trick-taking games helps illuminate both its familiar elements and unique innovations.

Bridge: Hokm shares Bridge’s fundamental structure—four players in fixed partnerships using a full 52-card deck, with 13 cards dealt to each player. Both games demand sophisticated partnership coordination and feature trump suits that can capture any non-trump card. However, Bridge’s elaborate bidding system, where partnerships communicate hand strength and determine both trump and a target trick count, contrasts sharply with Hokm’s streamlined approach. In Hokm, the Hakem simply declares trump unilaterally, eliminating the bidding phase entirely while maintaining the strategic depth of trump-based play.

Spades: Like Hokm, Spades features partnerships and trump-based trick-taking, making it perhaps the closest American equivalent. Both games emphasize aggressive trick-taking and partnership coordination. The key difference lies in trump determination: Spades fixes spades as the permanent trump suit, while players bid on their expected trick count. Hokm’s rotating trump declaration by the Hakem creates more dynamic gameplay, as the trump suit changes each deal based on one player’s assessment of their hand.

Hearts: While Hearts shares the basic trick-taking mechanics and uses the same deck size, it represents almost the opposite philosophy to Hokm. Hearts is an individual game focused on trick avoidance—players actively try to avoid taking certain cards that carry penalty points. Hokm, by contrast, emphasizes aggressive partnership-based trick collection. Hearts’ lack of trumps and partnerships makes it tactically simpler but psychologically different from Hokm’s cooperative-competitive dynamics.

Jass (Swiss): Perhaps the most intriguing comparison is with Jass, Switzerland’s national card game. Both games feature partnerships, rotating trump selection, and deep cultural significance in their respective regions. Jass shares Hokm’s emphasis on partnership coordination and strategic trump declaration. However, Jass typically uses a 36-card deck with unique card rankings (Jacks and Nines become high in trump suits), employs bidding mechanisms, and includes multiple game variants. Hokm’s consistent use of standard card rankings and streamlined rules make it more accessible while retaining comparable strategic depth.

Whist: As the historical ancestor of modern trick-taking games, Whist provides useful context. Like Hokm, it features partnerships and straightforward trick-taking without complex scoring. However, Whist predetermines trump through card exposure rather than player choice, missing Hokm’s crucial element of strategic trump selection. Hokm can be seen as an evolutionary development from Whist-style games, adding the psychological dimension of trump declaration while maintaining elegant simplicity.

The defining characteristic that sets Hokm apart from all these games is the Hakem system—the rotation of trump-declaring authority among players. This creates unique strategic dynamics where one player’s assessment of their hand directly shapes the entire deal’s character, introducing elements of both power and responsibility that don’t exist in other major trick-taking games.

Basic Setup and Objective

Players and Partnerships: Four players sit in a square formation, with partnerships consisting of opposite players (North-South vs. East-West). Partners work together to win the most tricks but cannot communicate directly about their cards.

Deck and Deal: The game uses a standard 52-card deck. Each player receives 13 cards, dealt in a specific pattern that varies by regional rules. The card ranking follows the standard hierarchy: Ace (high), King, Queen, Jack, 10, 9, 8, 7, 6, 5, 4, 3, 2 (low).

Winning Condition: The partnership that wins the majority of tricks (7 or more out of 13) wins the deal. Games typically consist of multiple deals, with the first partnership to reach a predetermined score (often 7 points) winning the match.

The Hakem System

The defining feature of Hokm is the Hakem (حاکم) system. The Hakem, meaning “ruler” or “judge,” is the player who declares the trump suit for each deal. This role rotates among players, creating shifting power dynamics throughout the game.

Trump Declaration: After examining their cards, the Hakem announces which suit will serve as trump for that deal. This decision is crucial—trumps can capture any non-trump card, regardless of rank, making suit selection a critical strategic choice.

Positional Advantage: The Hakem gains the privilege of leading the first trick, providing additional strategic control. However, this advantage comes with the burden of responsibility—poor trump selection can doom the partnership.

Gameplay Mechanics

Standard trick-taking conventions apply with trump modifications:

Players must follow the led suit if possible.
If unable to follow suit, players may play any card (including trumps).
The highest card of the led suit wins the trick unless a trump is played.
The highest trump wins if multiple trumps are played.
The winner of each trick leads to the next.

Information Dynamics: Hokm creates fascinating information asymmetries. While all players observe the cards played to each trick, the remaining cards in opponents’ hands remain hidden. The trump declaration provides some information about the Hakem’s hand strength in that suit, but skilled players can use deceptive declarations to mislead opponents.

Strategic Depth: Success requires implicit communication between partners through their card choices. Experienced players develop sophisticated signaling systems within the legal framework of the game, using specific card plays to convey information about hand strength and suit distribution. Players must operate on several strategic levels simultaneously:

Immediate tactics: Winning or losing individual tricks based on current information.
Information warfare: Concealing hand strength while gathering intelligence about opponents.
Long-term planning: Managing card resources across the entire 13-trick deal.
Partnership coordination: Supporting a partner’s strategies while pursuing individual objectives.

II. Model Architecture

The Shared Core

Converting all information to embeddings required creating a bespoke embedding system representing different data types:

Decomposed Embeddings: Rather than single card embeddings, I separated cards into distinct suit and rank embeddings, and concatenated them into one vector. This helps models learn fundamental card properties like high rank importance or trump suit significance.

Contextual Embeddings: Special segment, positional, and player embeddings provide complete context. Segment embeddings differentiate input parts like game history and current tricks. Positional embeddings convey event ordering. Player embeddings identify card players from relative perspectives (e.g., “my partner,” “right opponent”).

All embeddings feed into shared Transformer encoders producing single, rich public game state representations—the public_query.

The Actor: Card Selection

The Actor selects cards from agent hands using specialized mechanisms:

Hand Encoder: Separate Transformer encoders process agent hand cards.

Pointer Network: Pointer networks select actions by comparing public_query to each hand card, outputting scores. This approach proves far more efficient than guessing from all 52 cards while ensuring legal card play.

The Critic: Game State Evaluation

The Critic estimates game values—victory probabilities from current states. Multi-player imperfect-information games commonly employ “privileged” critics that, unlike actors, see all hands. This component accesses all player hands, using privileged information with public_query to predict game values.

III. Game Sample

Here’s a detailed sample game played by the policy against itself—all players using identical policies. I enjoyed providing commentary for each trick, and the game proved fascinating to analyze.

Game Info:
  - Hakem: Player 0
  - Trump Suit: Diamonds

Initial Hands:
  - Player 0: [5S, AS, 3C, 4C, 7C, TC, 6D, KD, 3H, 9H, TH, QH, KH]
  - Player 1: [2S, 8S, JS, QC, KC, 4D, 5D, 7D, 8D, 9D, JD, 2H, 4H]
  - Player 2: [3S, 4S, 7S, 9S, QS, KS, 2C, AC, 3D, TD, AD, 7H, AH]
  - Player 3: [6S, TS, 5C, 6C, 8C, 9C, JC, 2D, QD, 5H, 6H, 8H, JH]

----------------------------------------

--- Turn: Player 0 (Trick #1) ---
  - Hand: [5S, AS, 3C, 4C, 7C, TC, 6D, KD, 3H, 9H, TH, QH, KH]
  - Policy: 5S: 0.00%, AS: 99.67%, 3C: 0.04%, 4C: 0.00%, 7C: 0.00%, TC: 0.00%, 6D: 0.00%, KD: 0.00%, 3H: 0.12%, 9H: 0.03%, TH: 0.01%, QH: 0.08%, KH: 0.04%
  - Entropy: 0.0277, Critic Value: 0.4848
  - Action Played: AS
  - Reward Received: 0.00

--- Turn: Player 1 (Trick #1) ---
  - Hand: [2S, 8S, JS, QC, KC, 4D, 5D, 7D, 8D, 9D, JD, 2H, 4H]
  - Policy: 2S: 98.41%, 8S: 1.48%, JS: 0.10%, QC: 0.00%, KC: 0.00%, 4D: 0.00%, 5D: 0.00%, 7D: 0.00%, 8D: 0.00%, 9D: 0.00%, JD: 0.00%, 2H: 0.00%, 4H: 0.00%
  - Entropy: 0.0853, Critic Value: -0.5636
  - Action Played: 2S
  - Reward Received: 0.00

--- Turn: Player 2 (Trick #1) ---
  - Hand: [3S, 4S, 7S, 9S, QS, KS, 2C, AC, 3D, TD, AD, 7H, AH]
  - Policy: 3S: 97.86%, 4S: 0.76%, 7S: 0.83%, 9S: 0.55%, QS: 0.00%, KS: 0.00%, 2C: 0.00%, AC: 0.00%, 3D: 0.00%, TD: 0.00%, AD: 0.00%, 7H: 0.00%, AH: 0.00%
  - Entropy: 0.1270, Critic Value: 0.7863
  - Action Played: 3S
  - Reward Received: 0.00

--- Turn: Player 3 (Trick #1) ---
  - Hand: [6S, TS, 5C, 6C, 8C, 9C, JC, 2D, QD, 5H, 6H, 8H, JH]
  - Policy: 6S: 49.75%, TS: 50.25%, 5C: 0.00%, 6C: 0.00%, 8C: 0.00%, 9C: 0.00%, JC: 0.00%, 2D: 0.00%, QD: 0.00%, 5H: 0.00%, 6H: 0.00%, 8H: 0.00%, JH: 0.00%
  - Entropy: 0.6931, Critic Value: -0.6299
  - Action Played: TS
  - Reward Received: -0.00


# Commentary: As the Hakem, Player 0 makes the classic and optimal opening move: leading a non-trump Ace. The model's policy overwhelmingly favors the AS (99.67%), and the near-zero entropy (0.0277) reflects its absolute certainty. This play guarantees winning the trick, gathers information about the opponents' holdings in that suit, and does so without risking a valuable trump card. The other players correctly discard their lowest Spades, with Player 3's choice of TS over 6S being a minor but notable decision to shed a higher-ranking, non-winning card.

--- Turn: Player 0 (Trick #2) ---
  - Hand: [5S, 3C, 4C, 7C, TC, 6D, KD, 3H, 9H, TH, QH, KH]
  - Policy: 5S: 0.05%, 3C: 1.92%, 4C: 0.07%, 7C: 0.18%, TC: 0.22%, 6D: 0.01%, KD: 0.20%, 3H: 8.59%, 9H: 1.81%, TH: 0.78%, QH: 45.17%, KH: 41.01%
  - Entropy: 1.1684, Critic Value: 0.7800
  - Action Played: QH
  - Reward Received: 0.00

--- Turn: Player 1 (Trick #2) ---
  - Hand: [8S, JS, QC, KC, 4D, 5D, 7D, 8D, 9D, JD, 2H, 4H]
  - Policy: 8S: 0.00%, JS: 0.00%, QC: 0.00%, KC: 0.00%, 4D: 0.00%, 5D: 0.00%, 7D: 0.00%, 8D: 0.00%, 9D: 0.00%, JD: 0.00%, 2H: 90.43%, 4H: 9.57%
  - Entropy: 0.3156, Critic Value: -0.5770
  - Action Played: 2H
  - Reward Received: 0.00

--- Turn: Player 2 (Trick #2) ---
  - Hand: [4S, 7S, 9S, QS, KS, 2C, AC, 3D, TD, AD, 7H, AH]
  - Policy: 4S: 0.00%, 7S: 0.00%, 9S: 0.00%, QS: 0.00%, KS: 0.00%, 2C: 0.00%, AC: 0.00%, 3D: 0.00%, TD: 0.00%, AD: 0.00%, 7H: 97.38%, AH: 2.62%
  - Entropy: 0.1214, Critic Value: 0.6762
  - Action Played: 7H
  - Reward Received: 0.00

--- Turn: Player 3 (Trick #2) ---
  - Hand: [6S, 5C, 6C, 8C, 9C, JC, 2D, QD, 5H, 6H, 8H, JH]
  - Policy: 6S: 0.00%, 5C: 0.00%, 6C: 0.00%, 8C: 0.00%, 9C: 0.00%, JC: 0.00%, 2D: 0.00%, QD: 0.00%, 5H: 6.99%, 6H: 1.65%, 8H: 4.99%, JH: 86.37%
  - Entropy: 0.5299, Critic Value: -0.4925
  - Action Played: JH
  - Reward Received: -0.00

# Commentary: Leading again, Player 0 probes the Heart suit by playing the QH. The model is split between its QH (45.17%) and KH (41.01%), indicated by the high entropy (1.1684), suggesting it sees both as viable moves to draw out the Ace. The most strategically brilliant play of the game follows: Player 2, holding the AH, intelligently plays the 7H instead. The model's 97.38% confidence in this move demonstrates a learned collaborative strategy. It "ducks" to let its partner's Queen win, preserving its own Ace as the controlling card of the suit for a later, more critical trick. This is a perfect example of AI teamwork.

--- Turn: Player 0 (Trick #3) ---
  - Hand: [5S, 3C, 4C, 7C, TC, 6D, KD, 3H, 9H, TH, KH]
  - Policy: 5S: 0.02%, 3C: 0.74%, 4C: 0.02%, 7C: 0.06%, TC: 0.14%, 6D: 0.00%, KD: 0.06%, 3H: 6.29%, 9H: 1.85%, TH: 1.30%, KH: 89.51%
  - Entropy: 0.4618, Critic Value: 0.8749
  - Action Played: KH
  - Reward Received: 0.00

--- Turn: Player 1 (Trick #3) ---
  - Hand: [8S, JS, QC, KC, 4D, 5D, 7D, 8D, 9D, JD, 4H]
  - Policy: 8S: 0.00%, JS: 0.00%, QC: 0.00%, KC: 0.00%, 4D: 0.00%, 5D: 0.00%, 7D: 0.00%, 8D: 0.00%, 9D: 0.00%, JD: 0.00%, 4H: 100.00%
  - Entropy: -0.0000, Critic Value: -0.8137
  - Action Played: 4H
  - Reward Received: 0.00

--- Turn: Player 2 (Trick #3) ---
  - Hand: [4S, 7S, 9S, QS, KS, 2C, AC, 3D, TD, AD, AH]
  - Policy: 4S: 0.00%, 7S: 0.00%, 9S: 0.00%, QS: 0.00%, KS: 0.00%, 2C: 0.00%, AC: 0.00%, 3D: 0.00%, TD: 0.00%, AD: 0.00%, AH: 100.00%
  - Entropy: -0.0000, Critic Value: 0.7901
  - Action Played: AH
  - Reward Received: 0.00

--- Turn: Player 3 (Trick #3) ---
  - Hand: [6S, 5C, 6C, 8C, 9C, JC, 2D, QD, 5H, 6H, 8H]
  - Policy: 6S: 0.00%, 5C: 0.00%, 6C: 0.00%, 8C: 0.00%, 9C: 0.00%, JC: 0.00%, 2D: 0.00%, QD: 0.00%, 5H: 32.18%, 6H: 5.78%, 8H: 62.04%
  - Entropy: 0.8258, Critic Value: -0.7269
  - Action Played: 8H
  - Reward Received: -0.00

# Commentary: Player 0 correctly deduces that its partner holds the AH after the QH won the previous trick unchallenged. It confidently plays its KH (89.51% policy), a move designed to "cash out" a winner and hand the lead over to its partner. Player 2 is now forced to play its AH, as it's the only Heart remaining. This sequence showcases the Hakem team's perfect control and extraction of value from the Heart suit.

--- Turn: Player 2 (Trick #4) ---
  - Hand: [4S, 7S, 9S, QS, KS, 2C, AC, 3D, TD, AD]
  - Policy: 4S: 0.00%, 7S: 0.00%, 9S: 0.00%, QS: 0.09%, KS: 0.81%, 2C: 0.00%, AC: 94.85%, 3D: 0.02%, TD: 0.00%, AD: 4.22%
  - Entropy: 0.2318, Critic Value: 0.8462
  - Action Played: AC
  - Reward Received: 0.00

--- Turn: Player 3 (Trick #4) ---
  - Hand: [6S, 5C, 6C, 8C, 9C, JC, 2D, QD, 5H, 6H]
  - Policy: 6S: 0.00%, 5C: 22.27%, 6C: 3.60%, 8C: 43.12%, 9C: 13.12%, JC: 17.89%, 2D: 0.00%, QD: 0.00%, 5H: 0.00%, 6H: 0.00%
  - Entropy: 1.3912, Critic Value: -0.8623
  - Action Played: 8C
  - Reward Received: 0.00

--- Turn: Player 0 (Trick #4) ---
  - Hand: [5S, 3C, 4C, 7C, TC, 6D, KD, 3H, 9H, TH]
  - Policy: 5S: 0.00%, 3C: 97.93%, 4C: 1.59%, 7C: 0.15%, TC: 0.32%, 6D: 0.00%, KD: 0.00%, 3H: 0.00%, 9H: 0.00%, TH: 0.00%
  - Entropy: 0.1147, Critic Value: 0.8158
  - Action Played: 3C
  - Reward Received: 0.00

--- Turn: Player 1 (Trick #4) ---
  - Hand: [8S, JS, QC, KC, 4D, 5D, 7D, 8D, 9D, JD]
  - Policy: 8S: 0.00%, JS: 0.00%, QC: 72.64%, KC: 27.36%, 4D: 0.00%, 5D: 0.00%, 7D: 0.00%, 8D: 0.00%, 9D: 0.00%, JD: 0.00%
  - Entropy: 0.5868, Critic Value: -0.9992
  - Action Played: QC
  - Reward Received: -0.00

# Commentary: Now in control of the lead, Player 2 transitions to another suit, playing its AC with high confidence (94.85%). This is a power play to secure another guaranteed trick and continue stripping the opponents of high cards. The Critic value remains high for Team 0/2 (0.8462 for P2, 0.8158 for P0), indicating the AI understands it is in a commanding position.

--- Turn: Player 2 (Trick #5) ---
  - Hand: [4S, 7S, 9S, QS, KS, 2C, 3D, TD, AD]
  - Policy: 4S: 0.03%, 7S: 0.03%, 9S: 0.07%, QS: 5.88%, KS: 31.72%, 2C: 0.05%, 3D: 0.07%, TD: 0.01%, AD: 62.14%
  - Entropy: 0.8464, Critic Value: 0.9240
  - Action Played: AD
  - Reward Received: 0.00

--- Turn: Player 3 (Trick #5) ---
  - Hand: [6S, 5C, 6C, 9C, JC, 2D, QD, 5H, 6H]
  - Policy: 6S: 0.00%, 5C: 0.00%, 6C: 0.00%, 9C: 0.00%, JC: 0.00%, 2D: 96.59%, QD: 3.41%, 5H: 0.00%, 6H: 0.00%
  - Entropy: 0.1486, Critic Value: -1.0851
  - Action Played: 2D
  - Reward Received: 0.00

--- Turn: Player 0 (Trick #5) ---
  - Hand: [5S, 4C, 7C, TC, 6D, KD, 3H, 9H, TH]
  - Policy: 5S: 0.00%, 4C: 0.00%, 7C: 0.00%, TC: 0.00%, 6D: 98.88%, KD: 1.12%, 3H: 0.00%, 9H: 0.00%, TH: 0.00%
  - Entropy: 0.0616, Critic Value: 0.8033
  - Action Played: 6D
  - Reward Received: 0.00

--- Turn: Player 1 (Trick #5) ---
  - Hand: [8S, JS, KC, 4D, 5D, 7D, 8D, 9D, JD]
  - Policy: 8S: 0.00%, JS: 0.00%, KC: 0.00%, 4D: 32.10%, 5D: 20.01%, 7D: 28.31%, 8D: 10.91%, 9D: 3.92%, JD: 4.75%
  - Entropy: 1.5572, Critic Value: -1.0187
  - Action Played: 4D
  - Reward Received: -0.00

# Commentary: With a 4-0 lead, Player 2 makes a strategically decisive move: leading the Ace of the trump suit (Diamonds), but doesn't do it with full confidence (only 62%). The other good option is to play KS (at 32% probability), and this makes sense, because AS has been played. Ultimately, playing the Ace of the trump suit is chosen, and this forces the other players to play their Diamonds. A good reason to do that is to exhaust the opponents' trump cards, and aquiring information about their hands, and also increasing the value of its team's remaining high cards in other suits. The model's high Critic value (0.9240) shows it anticipates this aggressive play will cement its path to victory.

--- Turn: Player 2 (Trick #6) ---
  - Hand: [4S, 7S, 9S, QS, KS, 2C, 3D, TD]
  - Policy: 4S: 0.06%, 7S: 0.05%, 9S: 0.39%, QS: 7.21%, KS: 92.08%, 2C: 0.04%, 3D: 0.06%, TD: 0.10%
  - Entropy: 0.3104, Critic Value: 0.9084
  - Action Played: KS
  - Reward Received: 0.00

--- Turn: Player 3 (Trick #6) ---
  - Hand: [6S, 5C, 6C, 9C, JC, QD, 5H, 6H]
  - Policy: 6S: 100.00%, 5C: 0.00%, 6C: 0.00%, 9C: 0.00%, JC: 0.00%, QD: 0.00%, 5H: 0.00%, 6H: 0.00%
  - Entropy: -0.0000, Critic Value: -0.9479
  - Action Played: 6S
  - Reward Received: 0.00

--- Turn: Player 0 (Trick #6) ---
  - Hand: [5S, 4C, 7C, TC, KD, 3H, 9H, TH]
  - Policy: 5S: 100.00%, 4C: 0.00%, 7C: 0.00%, TC: 0.00%, KD: 0.00%, 3H: 0.00%, 9H: 0.00%, TH: 0.00%
  - Entropy: -0.0000, Critic Value: 0.9726
  - Action Played: 5S
  - Reward Received: 0.00

--- Turn: Player 1 (Trick #6) ---
  - Hand: [8S, JS, KC, 5D, 7D, 8D, 9D, JD]
  - Policy: 8S: 35.53%, JS: 64.47%, KC: 0.00%, 5D: 0.00%, 7D: 0.00%, 8D: 0.00%, 9D: 0.00%, JD: 0.00%
  - Entropy: 0.6507, Critic Value: -0.7711
  - Action Played: JS
  - Reward Received: -0.00

# Commentary: Continuing its offensive, Player 2 leads the KS, which is now at 92% confidence. With the AS already played in the first trick, this card is now the highest-ranking Spade and a highly likely winner. This move effectively clears the Spade suit of any remaining threats. The Critic value for Player 2 is now a dominant 0.9084, signaling that a 7-0 victory is highly probable.

--- Turn: Player 2 (Trick #7) ---
  - Hand: [4S, 7S, 9S, QS, 2C, 3D, TD]
  - Policy: 4S: 1.04%, 7S: 1.06%, 9S: 6.85%, QS: 89.95%, 2C: 0.40%, 3D: 0.17%, TD: 0.53%
  - Entropy: 0.4355, Critic Value: 0.9901
  - Action Played: QS
  - Reward Received: 0.00

--- Turn: Player 3 (Trick #7) ---
  - Hand: [5C, 6C, 9C, JC, QD, 5H, 6H]
  - Policy: 5C: 0.01%, 6C: 0.00%, 9C: 0.00%, JC: 0.07%, QD: 99.90%, 5H: 0.01%, 6H: 0.01%
  - Entropy: 0.0089, Critic Value: -0.9853
  - Action Played: QD
  - Reward Received: 0.00

--- Turn: Player 0 (Trick #7) ---
  - Hand: [4C, 7C, TC, KD, 3H, 9H, TH]
  - Policy: 4C: 0.00%, 7C: 0.00%, TC: 0.00%, KD: 99.98%, 3H: 0.00%, 9H: 0.00%, TH: 0.00%
  - Entropy: 0.0018, Critic Value: 0.9850
  - Action Played: KD
  - Reward Received: 0.00

--- Turn: Player 1 (Trick #7) ---
  - Hand: [8S, KC, 5D, 7D, 8D, 9D, JD]
  - Policy: 8S: 100.00%, KC: 0.00%, 5D: 0.00%, 7D: 0.00%, 8D: 0.00%, 9D: 0.00%, JD: 0.00%
  - Entropy: -0.0000, Critic Value: -0.9196
  - Action Played: 8S
  - Reward Received: -2.00

# Commentary: This final trick is a masterclass in risk and reward. Player 2 leads its QS, attempting to cash its last high card for the sweep. Player 3, out of Spades, is forced to make a defensive play, trumping with its QD to prevent the 7-0 loss. This is Team 1's last hope. However, the gamble fails spectacularly. Player 0 is also out of Spades and reveals the KD, a higher trump card. With supreme confidence (99.98%), Player 0 performs an "overruff," taking the trick, securing the 7-0 victory, and earning 2 points for the game.

=== GAME OVER ===
Final Score: Team 0 (7) - Team 1 (0)

This complete game demonstrates what appears to be the model’s sophisticated strategic understanding, from opening theory through partnership coordination to endgame execution. The AI successfully combines tactical card play with strategic partnership coordination, achieving the coveted 7-0 victory through what seems to be superior teamwork.

Teaching (tiny) LLMs to Play Text-Based Games Using RL (on a $300 GPU)

The Art of Safe Policy Updates: From REINFORCE to TRPO and PPO